LeetCode每日一题

两数之和

题目描述：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

1
2
3
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

1
2
输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

1
2
输入：nums = [3,3], target = 6
输出：[0,1]

题解：

(哈希表)O(n)

所用数据结构：C++中的哈希表——unordered_map<int,int> hash

hash[nums[i]] = i

只需循环一边nums数组，每步循环中：

  1. 判断哈希表中是否存在target-nums[i];
  2. 将nums[i]插入哈希表中；

这两步顺序不能交换，否则会出现同一个元素多次使用的情况。

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> res;
        unordered_map<int,int>hash;
        //hash的key = nums[i], value = i;
        for(int i = 0; i < nums.size(); i++)
        {
            int ano = target - nums[i];
            //count用来检查是否存在hash[ano]，即key=ano处是否存在value
            //判断哈希表中是否存在等于target - nums[i]的key，如果有，说明该key也在nums数组中。则输出hash[ano]
            if(hash.count(ano)) 
            {
                res.push_back(hash[ano]);
                res.push_back(i);
                break;
            }
            hash[nums[i]] = i;
        }
        return res;
    }
};

两数相加

题目描述：

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

1
2
3
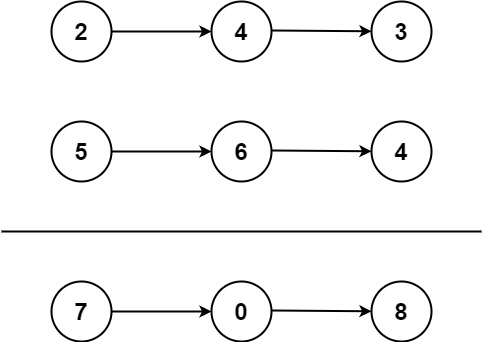
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

1
2
输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

1
2
输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

题解：

(模拟人工加法) O(n)
这是道模拟题，模拟我们小时候列竖式做加法的过程：

从最低位至最高位，逐位相加，如果和大于等于10，则保留个位数字，同时向前一位进1.
如果最高位有进位，则需在最前面补1.
做有关链表的题目，有个常用技巧：添加一个虚拟头结点：ListNode *head = new ListNode(-1);，可以简化边界情况的判断。
时间复杂度：由于总共扫描一遍，所以时间复杂度是 O(n).

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *res = new ListNode(-1); //添加虚拟头节点，简化边界情况的判断
        ListNode *cur = res;
        int t = 0;
        while(l1 || l2 || t)
        {
            if(l1) t += l1->val, l1 = l1->next;
            if(l2) t += l2->val, l2 = l2->next;
            cur = cur->next = new ListNode(t % 10);
            t /= 10; 
        }
        return res->next;
    }
};

无重复字符的最长子串

题目描述：

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

示例 4:

1
2
输入: s = ""
输出: 0

题解：

(双指针扫描)O(n)

定义两个指针i,j(i <= j)，表示当前扫描到的子串是[i,j]。扫描过程中，用哈希表unordered_map<char, int> hash来表示[i,j]中每个字符出现的次数。

例如：hash[ s[i] ]++ 表示哈希表 hash 中s[i]出现次数+1

线性扫描时：每次循环流程如下：

  1. 指针 j 向后移动一位，同时将哈希表中 s[j] 的个数加一：hash[ s[j] ]++;
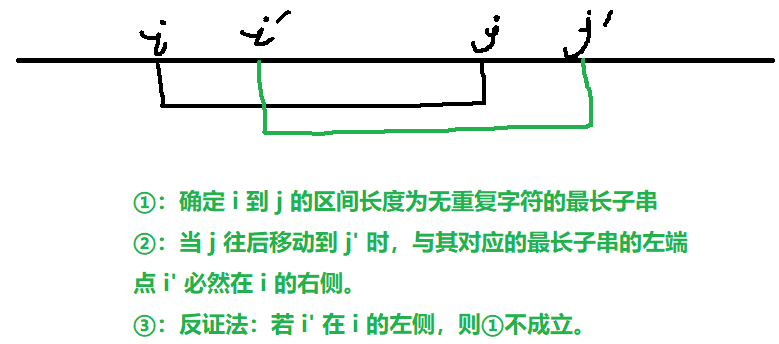
  2. 假设 j 移动前的区间 [i,j] 没有重复字符，则 j 移动后，只有 s[j] 可能出现2次。如果 s[j] 出现次数大于1，那么我们就不断向后移动 i，直到区间 [i,j] 中 s[j] 的个数等于1为止；

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> hash;
        int res = 0;
        for(int i = 0, j = 0; j < s.size(); j++)
        {
            hash[s[j]]++;
            while(hash[s[j]] > 1)
            {
                hash[s[i]]--;
                i++;
            }
            res = max(res, j - i + 1);
        }
        return res;
    }
};

最长回文子串

题目描述：

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

1
2
3
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

1
2
输入：s = "cbbd"
输出："bb"

示例 3：

1
2
输入：s = "a"
输出："a"

示例 4：

1
2
输入：s = "ac"
输出："a"

题解：

首先考虑回文串一共有几种？

  1. 长度为偶数：两两配对，例如aabb，ccddee。
  2. 长度为奇数：除了最中间的单独一个元素，其他两两配对，例如a，aabcc

  • 长度为奇数：

    假设已存在长度为奇数的回文子串，并且该回文子串的最中间的元素为i，设置两个指针l和r： l = i - 1，r = i + 1

    l和 r分别从i的左右两边出发，若不满足l >= 0 && r < s.size() && s[l] == s[r]，则说明找到了该回文子串的左右端点，则该回文子串的长度为：r - l - 1

  • 长度为偶数：

    偶数情况与奇数相同，只需要将l和r设置为：l = i，r = i + 1即可

整体：

将i所指的每一个字符都当作某一个回文子串最中间的值(奇数)，或者最中间的两个值中的一个(偶数)，只需遍历一边原字符串S，即可找到最长的回文子串。

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    string longestPalindrome(string s) {
        string res;
        for(int i = 0; i < s.size(); i ++)
        {
            int l = i, r = i + 1;
            while(l >= 0 && r < s.size() && s[l] == s[r]) l--, r++;
            if(res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);

            l = i - 1, r = i + 1;
            while(l >= 0 && r < s.size() && s[l] == s[r]) l--, r++;
            if(res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);
        }
        return res;
    }
};

Z字形变换

题目描述：

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

1
2
3
P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：

1
string convert(string s, int numRows);

示例 1：

1
2
输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

示例 2：

1
2
3
4
5
6
7
输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I

示例 3：

1
2
输入：s = "A", numRows = 1
输出："A"

题解：

时间复杂度：O(n)

这题考察的是找规律和等差数列

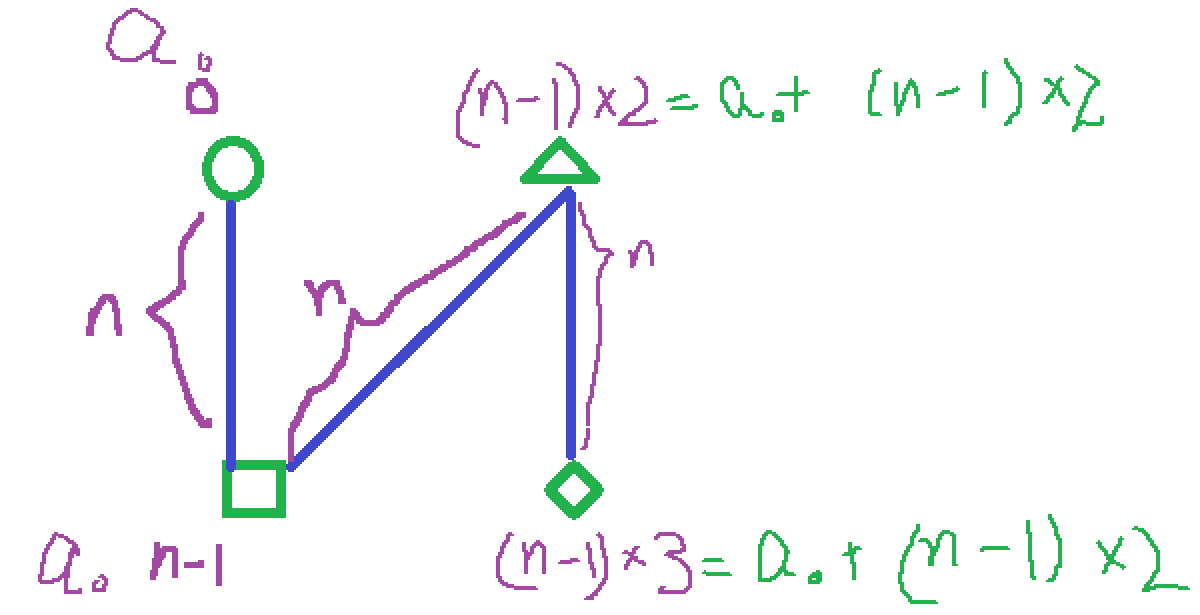
我们可以让numRows = 4，并观察首行，不难发现，首行的每个元素之间，公差为2n - 2。

1
2
3
4
0     6       12
1   5 7    11 ..
2 4   8 10
3     9

对于末行来说，元素之间的公差也为2n - 2 .

而由于第i行(0 < i < numRows - 1)是由竖线上的元素和斜线上的元素共同构成，我们需要单独分开来看

  1. 对于竖线上且处于同一行的元素：元素间公差为2n - 2
  2. 对于斜线上且处于同一行的元素：元素间公差也2n - 2

不难看出，对于第i行(0 < i < numRows - 1)，只需要每次交替地输出即可

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    string convert(string s, int numRows) {
        string res;
        if(numRows == 1) return s;
        int d = (numRows - 1)*2;
        for(int i = 0; i < numRows; i++)
        {
            if(i == 0 || i == numRows - 1)
            {
                for(int k = i; k < s.size(); k += d) res += s[k];
            }
            else
            {
                for(int k = i, j = d - i; k < s.size() || j < s.size(); k += d, j += d)
                {
                    if(k < s.size()) res += s[k];
                    if(j < s.size()) res += s[j];
                }
            }
        }
        return res;
    }
};

整数反转

题目描述：

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

1
2
输入：x = 123
输出：321

示例 2：

1
2
输入：x = -123
输出：-321

示例 3：

1
2
输入：x = 120
输出：21

示例 4：

1
2
输入：x = 0
输出：0

题解：

时间复杂度分析：一共有 O(logn)位，对于每一位的计算量是常数级的，所以总时间复杂度是 O(logn).

需要注意，因为int型整数逆序后可能会溢出，所以我们要用long long记录中间结果

在C++中，可用INT32_MAX表示32位的最大范围，对应最小范围为INT32_MIN.

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int reverse(int x) {
        long long res = 0;
        while(x != 0)
        {
            res = res * 10 + x % 10;
            x /= 10;
        }
        if(res > INT32_MAX || res < INT32_MIN) return 0;
        return res;
    }
};